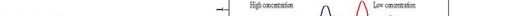MedicineLakex

 

Microsoft word - panetta oceans 12 manuscript pdf format.doc

Acoustic scattering to measure dispersed oil droplet size and sediment particle size Paul D. Panetta1,2, Leslie G. Bland1,3, Grace Cartwright2 and, Carl T. Friedrichs2 1Applied Research Associates, Inc. P.O. Box 1346, 1208 Greate Rd. Gloucester Pt. VA 23062 2Virginia Institute of Marine Science P.O. Box 1346, 1208 Greate Rd. Gloucester Pt. VA 23062 3University of Virginia Charlottesville, VA 22904 Abstract— The use of sound waves in oceanographic in field deployments the LISST becomes fouled by biological
environments is well established including active sonar growth. Acoustic technologies in oceanographic environments
applications for mapping seafloors, for submarine detection, and
are effective at very high concentrations in the water column, for passive listening. Acoustic waves have been used for many
in consolidated sediments and solids. Because of the access to years to study the ocean, including detecting and identifying
much higher concentrations and resistance to bio-fouling, objects in the water column, and the measuring the seafloor and
sub seafloor properties. One of the key parameters of the acoustic
acoustic instruments are commonly used to measure current field is the amplitude of the wave which scatters from the seafloor
speed using the Doppler shift from suspended particulates and or from objects in the water column. The amplitude, time of
suspended sediment concentration. While acoustic instruments flight, and frequency response can be used to map the seafloor,
work well in practical applications, measuring the particulate measure current flow, or to detect and classify objects in the
size is currently limited by the lack of theoretical understanding water column. In addition to these standard uses, acoustics can
of the scattering of the acoustic field and the complicated also be used to size particulates including sediment, oil droplets
interdependence of attenuating mechanisms to the and gas bubbles in the water. Our particular application for this
experimentally measured parameters. Research work is work is to detect, classify, and size sediment particles and
ongoing by the authors [1] and others [2,3] to develop high separately, oil droplets suspended in the water column using
knowledge of the acoustic backscattering and attenuation.
frequency particle sizing methods. For this paper we focus on Specifically, we have measured and separated the absorption,
studying the contributions to the attenuation with applications single scattering and multiple scattering contributions to to oil droplets and suspended sediment.
attenuation measurements. Our results show that the absorption
dominates the attenuation at low ka values << 1 and multiple
scattering and particle-particle interactions dominate at higher
II. ACOUSTIC INTERACTIONS WITH PARTICULATES ka values when ka > 1 with a transition between theses ranges
depending on the concentration of the suspensions. The physics
Several properties of an acoustic field can be used to has been proven out on silica particles in water and work is
ongoing on suspended sediment and suspensions of oil droplets.
measure the characteristics of a particle suspension. These properties include attenuation, backscattering, and the speed of Index Terms—acoustic, particle size, attenuation, scattering
sound. Physically, the attenuation of transmitted acoustic field and speed of sound are determined from waves that traverse across the media and received by a second transducer Figure 1b). Backscattering is the portion of the field which is The most common method to measure particulate size in scattered directly back to the transmitting transducer. The oceanographic environments is laser scattering and backscattered field at various concentrations for 70 microns transmission with the popular Laser In-Situ Scattering and glass spheres ranging from 5 to 40 wt% is shown in Figure 1c. Transmissometery (LISST) instrument. The LISST works well A fourth quantity that can be measured is the scattered sound in low concentration suspensions below 250 mg/L (400 ppm) which travels as a diffuse field, for suspended mud and 700 ppm for oil droplets in water, but

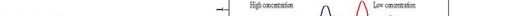
fluid. In addition, energy can be lost through heat generated by friction as the particle is moved through the viscous fluid. Changing the direction of motion of the particle as it oscillates (accelerating and decelerating the particle) also removes energy from the acoustic field. If the particle is not rigid, then it can also change shape as the acoustic field moves through the media, causing additional energy losses. These mechanisms can be broadly categorized as scattering losses and damping or absorption losses. While there are many contributions to energy loss as the acoustic field interacts with the fluid and the solid phases of the slurry, the dominant contributions are (1) the heat loss due to the friction between the viscous fluid and the particles as they move through the slurry, (2) energy loss to accelerate and decelerate the particle as it oscillates, and (3) the scattering of sound out of the propagating field. These three dominant loss mechanisms will now be described including the regimes where each is dominant. After this description of Fig. 1 (a) Schematic of ultrasonic measurement apparatus, (b) through transmitted RF signal for attenuation and velocity determination, (c) directly attenuation, the appropriate contributions to the backscattering backscattered signal, and (d) diffuse field signal. and diffuse field will be discussed. Acoustic fields propagating in suspensions suffer attenuation shown in Figure 1d. Here the coherent reflections from the due to viscous and thermal damping, and scattering opposite side of the container can be seen in the early time mechanisms. Attenuation of sound propagation in suspensions (<200 microseconds). The amplitude of the diffuse field builds can be divided into the following four major regimes. up in the 100 to 400 microseconds range, and then decays in 1) Viscous regime: time. This decay is a direct measure of the absorption When k R 1 and Re  R /  R   /(2) 1, attenuation contribution to the attenuation. Notable in these acoustic signals is the very large time has been shown to scale with 2 R 2 / . Where kc is the wave range they span. The coherent signal used for determining number = 2 , R is the particle radius,  is the boundary attenuation and velocity cover approximately 1 microseconds. layer thickness,  is the frequency, l and  are the density The direct backscattered, which is in incoherent summation of and viscosity of the fluid phase, respectively. individual scattering events spans approximately 130 2) Inertial regime: microseconds, while the diffusely scattered field persists for When k R 1and Re >> 1, the Basset history term begins to many milliseconds. The physics governing the propagation of these fields is different in each time domain and is dominated influence the particle drag. Consequently, the drag becomes by specific properties of the suspension. dominated by inertia through the added mass effect. However, These measurements have been applied for many decades the added mass force is conservative and does not contribute to study solid-liquid suspensions and elastic solids with varying to losses, and the dominant loss term is the in-phase degrees of success. Performing the conventional component of the Basset force. In this regime, the attenuation measurements of attenuation, backscattering, and speed of scales with  / R . sound are relatively simple. The more difficult task is to 3) Multiple scattering regime: accurately model the mechanisms contributing to the measured When k R 1, the field scatters geometrically. In an attenuation and to understand the effects of the different assembly of many randomly arranged particles, the field will attenuating mechanisms on the various measurements. The scatter randomly and thus penetrate poorly (high attenuation). inversion of the theory for comparison with experimental Here attenuation scales with 4 results to provide the specific characteristics of the slurry can be computationally intensive and inaccurate. When describing 4) Resonance Regime: acoustic wave propagation in slurries, there are several Particles may exhibit resonance characteristics and the important factors, including, particle size and shape, frequency of the first mode of resonance can be approximated concentration, heterogeneities, and the degree of multiple as the inverse of the time the acoustic field takes to travel scattering and particle-particle interactions present. twice the diameter of the particle. For particles that have sufficiently higher acoustic velocity, transition to multiple The following sections describe the physics governing the scattering will set in first. However, most plastic particles will attenuation, backscattering and diffuse field. often exhibit resonance absorption at frequencies A. Attenuation below k R  1. As an acoustic field moves through a solid-liquid Attenuation has been used widely and successfully to suspension, the fluid and the solid attenuate the field through characterize dilute slurries. Allegra and Hawley [4] provided several different mechanisms. Specifically, the acoustic field the groundbreaking theoretical treatment for solid-liquid can be scattered at the interfaces between the particle and the suspensions. Their model accounts for the attenuation due to viscous damping, as a particle moves and changes shape, the particle radius. Agreement between the model results and the thermal loss as heat is exchanged between the acoustic field experimental results were quite good, which indicates that and the particle, and the scattering loss as the propagating wave multiple scattering terms are important. is scattered at the interfaces between the fluid and the solid The main obstacles for implementing attenuation particles. However, they obtained good agreement between measurements to slurry characterization have proven to be the experimental measurements of attenuation and theoretical mathematical complexities of accounting for multiple predictions only at low concentrations. Furthermore, their scattering at high concentrations, and the accompanying theory lacks an explicit term for the backscattering amplitude complex nature of the inversion process. In addition, the and does not incorporate particle size distributions, acoustic attenuation measurements require careful alignment of hydrodynamic effects of relative motion between particle and transducers, further decreasing the accuracy and precision of fluid, and contributions from multiple scattering. the methodologies based on attenuation alone. In addition to the work of Allegra and Hawley, there have been a significant number of researchers who have studied B. Backscattering wave propagation in various suspensions, including Backscattering measurements have several advantages over Commander and Prosperetti [5], Soong et al. [6], Challis et al. attenuation measurements, including insensitivity to alignment [7], Holmes et al. [8], Atkinson and Kytomaa [9, 10], and of the transducer and small propagation distances, thus making Kytomaa [11]. In recent studies of attenuation in sols and gels, them ideal for characterizing highly attenuated slurries. In Holmes and Challis [12,13] showed that the single scattering addition, since the direct backscattered field usually can be models were inadequate at high concentrations. Recently, described by single-scattering processes, the mathematical Dukin and Goetz [14] studied two particle sizes at low inversion processes is often more simple and stable than those concentrations. Notable work has been performed by Dave used for attenuation. Figure 1c shows typical backscattered Scott in industrial applications where he showed that the signals in a solid-liquid suspension. attenuation can be used for particle size determination at low Backscattering in suspensions has been less thoroughly concentrations. [15,16,17]. Furthermore, he produced data studied, relative to attenuation, with the efforts largely focused which showed a deviation for the Allegra and Hawley model at on geologic and oceanographic applications. Notably, Hay and high concentrations, indicating that multiple scattering is Mercer (1985) used the theory developed by Allegra and significant and needs to be accounted for in industrial slurries. Hawley [4] to explicitly determine the backscattering In recent work, Spelt and coworkers have shown excellent amplitude as a function of the elastic properties of the scatterers theoretical progress in developing a model for slurries that and the viscous fluid. They further extended their work to accurately predicts attenuation at low concentrations for include particle size distributions of sand particles in specific weak scatterers [18]. In addition, they extended their suspension. In addition, He and Hay [22] accounted for the models using an effective medium technique that shows irregular shapes of sand particles by performing an ensemble promise for accounting for the effects particle-particle average of the scattered pressure. They obtained good interactions on attenuation in concentrated slurries. Their agreement with experimental results for sand particles in results show good agreement in slurries at concentrations up to suspension up to kR 1. Hay [23] further studied only 30 volume % solids, indicating that it is likely that the backscattering in flowing suspensions and observed evidence theory does not account for enough of the multiple scattering to of concentration fluctuations in the turbulent flow. These provide accurate predictions at higher concentrations. They theories were then applied to the inversion problem of also indicated that their approach had limited applicability for determining the concentration and size of sand particles in strongly scattering particles with elastic properties that vary suspension [24 Crawford and Hay 1993]. Reasonable significantly from water. Furthermore, their techniques are agreement was obtained for low concentrations and particle applicable only for dilute suspensions, and the inversion size for a wide range of materials including fused quartz and process is sensitive to the complex resonance behavior of the granite. Their level of agreement was poor at higher particles in slurries and the frequency range for which the comparison is made. Even though, their theoretical treatment Other efforts to use backscattering to characterize sediment has limitations, it represents significant progress towards have been undertaken by Thorne and Hardcastle [25] where including multiple scattering effects in the theoretical they performed in-situ sampling during measurements of description of attenuation in slurries. turbulent sediments. Agreement between experimental results Researchers have studied multiple scattering for several and theoretical predictions of particle size and concentration decades. Notably, Davis [19] studied the effects of multiple were quite good over a large range of concentrations. At high scattering on attenuation in suspensions and emulsions. In his concentrations, the inversion technique was difficult to perform studies, he coupled the single scattering amplitude developed due to a high attenuation. This difficulty could be related to the by Allegra and Hawley [4] and the multiple scattering approach fact that the theory relied on a single scattering approach and described by Waterman and Truell [20]. Varadan et al. [21] the irregularly shaped particles were assumed to be spherical. modeled multiple scattering by bubbles in water using a T- The irregular shape of sand particles was modeled by Matrix approach and Lax's quasi-crystalline approximation for Thorne et al. [26], who used a boundary element method and a scattering for kR <1, where k is the wave number and R is the finite element method to numerically model the complicated particle shapes. An alternative approach has been employed by Schaafsma et al. [27], who used an equivalent spherical scatter particles and fish, showing applicability to marine method Schaafsma and Hay [28] to model the irregular shape environments. They also showed that multiple scattering can of sand particles and showed much better agreement at be important and should not be neglected. An important frequencies where strong multiple scattering can be significant outcome of their work was the study of the correlation of the backscattering with time. Page has also advanced his work on Recently, an attempt at accounting for inhomogeneities in diffusing acoustic wave spectroscopy (DAWS). Specifically, sediments was performed by Guillon and Lurton [29] where they have accounted for particle motion and show good they modeled the backscattering from buried sediment layers agreement between experiments and theory [39]. and accounted for the losses at interfaces between layers. One A particularly significant theoretical advancement is given of the major problems of this approach is the complexity of the by a series of papers by Turner and Weaver [40, 41, 42, 43] inversion process. where they modeled the backscattering in polycrystalline materials using a radiative transfer approach for all regions of backscattering from early-occurring single scattering through C. Diffuse Field Absorption late-occurring multiple scattering. While these results are Another aspect of the scattered field that is intimately promising, it is evident that the characteristics of the diffuse related to the properties of the particulate suspension is the field are rich with information and that theoretical work and portion that undergoes multiple scattering and diffuses through experimental applications to particle size distributions are not the media. These signals arrive at the detector after several yet well developed. milliseconds as compared to the direct backscatter signals which typically arrive in a few 10's of microseconds [30]. III. ANALYSIS METHODS After multiple scattering events, the acoustic diffuse field develops [31], and a portion of the scattered wave eventually A. Separation of Attenuation Mechanisms returns to the transducer. Buildup of this field is governed by a The acoustic measurements of attenuation, backscattering, diffusivity term that is a function of the mean free path and, and the diffuse field are sensitive to particle properties in thus, is related to the size of the scatterers. The decay rate is suspensions. To create a method to characterize particulate related to the energy absorbed from the acoustic field (see suspension, one must separate these attenuating mechanisms so Figure 1d) and is also a function of particle type, size and they can be studied and modeled individually. The authors concentration. The loss mechanisms in the long time limit for developed methods to isolate these attenuating mechanisms in the diffuse field are dominated only by viscous losses and dilute and highly concentrated slurries [1]. A brief description particle motion, with little or no scattering losses. of the scientific basis behind the methods used to separate and One of the appealing aspects of the diffuse field isolate attenuation mechanisms will be given in this section. measurement of absorption is that it can also be performed with It was previously mentioned that (i) the attenuation one or more transducers and sensor alignment is not important. measured from a "through transmitted" signal is a function of In addition, the insonified volume can be larger than for the absorption, single scattering, multiple scattering, and particle- backscattering for the same frequency because the wave travels particle interactions,(ii) the backscattering is a function of outward as a diffusely propagating wave. These measurements absorption and single scattering, and (iii) the diffuse field is a are especially appealing because they can be used to probe the function of the absorption only. The second point about the absorptive properties of the particles and thus can be used to backscattering is an assumption that may or may not be valid isolate specific mechanisms when used in combination with the under certain circumstances. We will accept this assumption as attenuation and backscattering. correct for the purposes of this paper and subsequent analysis. While the majority of applications of the diffuse field An illustration showing these acoustic signals and equations for absorption measurements have focused on characterizing calculating the attenuation is displayed in Figure 2. The solids, Weaver and Sachse [32] focused their work on slurries. attenuation from the through transmitted signal is calculated by In their study, it was significant that measurements were comparing the signal in the slurry to a reference signal in water. performed on slurry containing strongly scattering glass The attenuation for the backscattering and diffuse field is spheres at a concentration of 62 wt %. In addition, Page et al. calculated by measuring the decay rate of the scattered signals [33, 34] reproduced the work of Weaver and Sachse and then at individual frequencies. Here  is the attenuation, f is the applied the diffuse field technique to measure particle motion acoustic frequency, z is the separation distance of the in a non-stationary suspension. Panetta has also utilized these transducers, D is the diffraction correction for a circular piston measurements to characterize solid liquid suspensions and transducer,  is the transducer efficiency, (f) is the Fourier isolate specific attenuation mechanisms [38]. amplitude of the received signal,  is the decay rate and v is the While the simple model employed by Weaver and Sachse [32] described the fluid motion in a matrix of immobile The attenuation as a function of frequency for 70 micron particles, recent work by Rosny and Roux [36, 37, 38] takes silica spheres in water at 10 wt% for each of these into account the effects of the particle motion on the diffuse measurements is shown in Figure 3. The through transmitted field characteristics. They obtained excellent agreement attenuation is between experiments and theory for dilute solutions of moving Attenuation velocity The results from this process are shown in Figure 4 where Absorption and single and multiple scattering each contribution to attenuation is plotted as a function of frequency. As expected, the frequency dependence of the   f  1 ref  f  ref  f  slurry  f  slurry  slurry   slurry   multiple scattering increased to 3.5, the single scattering increased to 2.1, and the absorption dependence on frequency remained constant. Absorption and single scattering 70 um SiO2 spheres in water (10 wt%)
 BS  f   f  Time (microseconds) Multiple scattering and particle particle interactions   f   DF  f  DF  f Fig. 2 Ultrasonic measurements of attenuation suing the through transmitted signal, the backscattering, and the diffuse field. The associated equations are shown on the right. Single scattering highest; the backscattering attenuation is next, followed by the diffuse field measurement of the attenuation. The frequency response of the attenuation is shown in Figure 3 and within the included table where the through transmitted attenuation has a power of 2.5, backscattering 1.7, and diffuse field 0.3. These Fig. 4. The isolated attenuation mechanisms plotted as a function of powers indicate the through transmitted attenuation is frequency. The power of the frequency dependence increased as expected. dominated by multiple scattering, the diffuse field by absorption, with the backscattering containing both scattering and absorption contributions. A. Silica Suspensions The dependence of the attenuation on each mechanism is The dependence of these mechanisms on concentration is shown in the equations below. These equations can be shown in Figure 5 and reveals the true power and insight this rearranged to solve for the individual contribution as follows: method provides into understanding the acoustic properties of the suspension. For 70 microns glass spheres in water at 5 Through _ transmission  Multiple _ scattering   Single_scattering   Absorption   (1) MHz, the single scattering contribution to attenuation Backscattering _ decay  Single _ scattering   Absorption   dominates below 10 wt % while the multiple scattering Diffuse _ field _ decay  Absorption  contributions to attenuation dominate above 15 wt%. These results show why the commercial acoustic instruments, which Multiple _ scattering  f  Through _ transmission  f  _ decay  f  rely on attenuation measurements dominated by multiple Single _ scattering  f  _ decay  f  Diffuse _ field _ decay  f  scattering and particle-particle interactions, become inaccurate at high concentrations. Absorption  f  Diffuse _ field _ decay  f  These results summarize the fundamental science underlying acoustic particle characterization, provide the insight needed to better use commercial instruments, and 70 um SiO 2 spheres in water (10 wt%)
indicate where the commercial instruments are likely to fail or become inaccurate. Through transmitted 70 um Glass Spheres
Multiple scattering and particle particle interactions Attenuat 0.5
Single scattering Atten 0.1
Fig. 3 The attenuation mechanisms as a function of frequency. Fig. 5. The isolated attenuation mechanisms plotted as a function of concentration. Above 15 wt% the multiple scattering gang particle-particle interactions dominate the attenuation Initial results applying these methods to oil suspensions by measuring the attenuation of the backscattered signal are in the next section. Early indications in consolidated sediment cores shows the same methods may be used to determine the grain size of sediment in the seafloor. Detailed results will be in future publications. B. Oil Dispersions Sonar was used during the recent blowout and associated oil leak from the Deepwater Horizon incident to image the plume and calculate the flow rate. In the case of the Deepwater Horizon blowout they did not have the monitoring tools to determine the efficacy of the 1.1 million gallons of Corexit Fig. 6. The acoustic test chamber for oil-dispersant mixtures. The syringe was 9500 dispersant injected directly into a flowing plume of oil used to uniformly mix the suspensions. The acoustic transducer is shown in and natural gas. Dispersants main effect is to decrease the the right figure pointing vertically down. surface tension at the oil-water interface causing the oil to form droplets smaller than 70 microns so they can remain in the The oil-dispersant mixture was created in a separate chamber water column long enough to be consumed by naturally by inserting the dispersant into the chamber full of water with a occurring bacteria. pipet. The dispersant-water mixture was then mixed with by There is a need to develop a deeper understanding of the repetitively drawing and emptying it from the syringe. Then, scattering of acoustic waves from particulates, sediment, and oil was added by first drawing approximately 20 cc of the oil droplets to effectively utilize the vast array of sonar and dispersant-water mixture into the syringe then drawing the oil marine acoustic instruments. Specifically, to effectively size into the partially full syringe. The syringe with the oil- suspended particles in the water column and in consolidated dispersant-water mixture was then placed back into the sediments in the seafloor, it is important to understand the chamber and repetitively filled and emptied to uniformly contributions from single scattering and multiple scattering as disperse the oil. Care was taken to ensure the total oil well as the absorption contributions to attenuation that control concentration was below the striation limit of the LISST which the wave propagation, especially in high concentration systems was approximately 700 ppm. The image of the acoustic experienced in the seafloor sediment and subsea blowouts backscattering for each ping for the chemically dispersed oil is experienced during the Deepwater Horizon incident. shown in Figure 7b. The ability for the dispersant to keep the Measurements were performed at both the Department of oil in the water column can be seen by the scattering from the Interior Ohmsett outdoor wave tank in New Jersey, and at the suspended droplets indicated by the orange/red region Applied Research Associates, Inc. labs on the Virginia Institute extending to 100 seconds. The dispersant and water were of Marine Science Campus. incorrectly mixed prior to adding the oil diminishing the The acoustic test chamber is shown in Figure 6. To ensure efficiency of the dispersant to disperse the oil. Individual good mixing of the oil-water-dispersant, we suctioned the droplets can also be seen as streaks across the image. mixture into a 60 cc syringe multiple times prior to performing Crude oil in water our measurements. A water mixture was mixed thoroughly within the acoustic test chamber while it was within the LISST testing area in order to calibrate the oil droplet size. Immediately after mixing with the syringe, the acoustic transducer was inserted into the chamber pointed down and data collection was started immediately. The acoustic data from multiple "pings" every 0.1 seconds for 300 seconds are Dispersant and Oil DOR 1:4 shown in Figure 7a for oil and oil-dispersant mixtures respectively. The mixture of oil droplets caused the acoustic wave to scatter, creating a bright orange/red pattern between zero and 30 seconds. After 30 seconds, scattering from the droplets caused distinguishable orange/red streaks. As more droplets floated up towards the surface, the streaks caused by the droplets generally pointed up with some streaks pointing left to right or down presumably from random motion in the Fig. 7. Acoustic images of the scattering from oil droplets in water over chamber. The droplets continued to move through the field of 300 seconds. An individual ping is shown on the right hand side of each figure. view of the transducer up to 250 seconds. The raw acoustic The red/orange regions are high scattering and the black is low scattering. The signal approximately 10 seconds after the transducer was long tracks are individual droplets as they float through the field of view of the inserted is shown at the right of the image. 5 MHz transducer. These images visually confirm the ability of the dispersant to keep oil in the water column over an extended period of time. To effectively size the droplets, we analyzed the raw acoustic waveforms shown on the right hand side of Figure 7 by determining the rate of decay of the acoustic signal. The signal was analyzed when oil remained within the water column of the testing chamber, often within the first 50 seconds. After this time, most of the oil droplets would have reached the top of the chamber. A ping range of approximately 15 to 20 seconds was taken within the data and a linear regression was fit over the data. The attenuation for isolated drops in water is given by the following equation [44]: Fig. 8. The comparison between our acoustic determination of the droplet size and the LISST determination. The inset shows the droplet size distribution from the LISST measurements. We have shown the contributions to acoustic attenuation can be separated and isolated through multiple measurements for silica particles in water. The multiple scattering and particle- particle interactions dominate the attenuation at high kR and concentration. The absorption dominated the attenuation at e = extinction cross section = sum of the scattering low kR with sing scattering dominating the attenuation at cross section and the absorption cross section intermediate kR values. These methods have been applied to a = droplet radius oil dispersions to study the efficacy of dispersants to keep oil in the water column. Applications to sediment will be fr = resonance frequency published later.  = damping constant at fr 0 = speed of sound  = ratio of specific heat at constant pressure and The authors would like to thank Wayne Reisner for fabricating the sample chambers, Randy Belore from S.L.Ross, P = hydrostatic pressure Al Guarino from Mar, Inc. for assistance at Ohmsett and Kyle = density of water Winfield for assistance with the experimental measurements. kr = wave vector at the resonant frequency The resonant frequency for 100 micron oil droplets is 0.055 MHz. At our operating acoustic frequency of 5 MHz, [1] Paul D. Panetta "Ultrasonic Characterization of Solid-Liquid which is much greater than the resonant frequency, the Suspension" US 7,739,911, 2010 attenuation is proportional to the droplet size, a. Thus, we can [2] Thorne, P. D., and D. M. Hanes (2002), A review of acoustic directly relate the attenuation to the droplet size. Using this measurement of small-scale sediment processes, Continental linear relationship, we then calculated the expected droplet size Shelf Research, 22(4), 603-632. based on our acoustic measurements. The comparison between [3] Thorne, P. D., and R. Meral (2008), Formulations for the our acoustic predictions of droplet sizes with the droplet size scattering properties of suspended sandy sediments for use in the measured from the LISST is shown in of Figure 8. The inset application of acoustics to sediment transport processes, shows the droplet size distribution determined from the LISST. Continental Shelf Research, 28(2), 309-317. While there is some spread, the relationship is quite good [4] Allegra, J.R. and S.A. Hawley. 1972. "Attenuation of Sound in considering some of the data is from Ohmsett and some from Suspensions and Emulsions: Theory and Experiments." The lab measurements using two different configurations. Journal of the Acoustical Society of America, 51(5): 1545-1564. [5] Commander, K.W. and A. Prosperetti. 1989. "Linear Pressure Waves in Bubbly Liquids: Comparison between Theory and Experiments." Journal of the Acoustical Society of America, 85(2): 732. [6] Soong, Y., A.G. Blackwell, R.R. Schehl, M.F. Zarochak, and [25] Thorne, P.D. and P.J. Hardcastle. 1997. "Acoustic J.A. Rayne. 1995. "Acoustic Characterization of Three-Phase Measurements of Suspended Sediments in Turbulent Currents Slurries." Chemical Engineering Communications, 138: 213- and Comparison with In Situ Samples." Journal of the Acoustical Society of America, 101(5): 2603. [7] Challis, R. E., M J W Povey, M L Mather, and A K Holmes, [26] Thorne, P.D., S. Sun, J. Zhang, I. Bjorno, and Mazoyer. 1997. Ultrasound techniques for characterizing colloidal Dispersions, "Measurements and Analysis of Acoustic Backscattering by REPORTS ON PROGRESS IN PHYSICS, Rep. Prog. Phys. 68 Elastic Cubes and Irregular Polyhedra." Journal of the Acoustical Society of America, 102(5): 2705. [8] Holmes, A.K., R.E. Challis, and D.J. Wedlock. 1993. "A Wide [27] Schaafsma, A.S. 1992. "Attenuation spectroscopy of suspended Bandwidth Study of Ultrasound Velocity and Attenuation in sediment suspensions", Journal of the Acoustical Society of Suspensions: Comparison of Theory with Experimental America 92, 2308. Measurements." J. of Colloid and Interface Sci, 156: 261-268. [28] Schaafsma, A.S. and A.E. Hay. 1997. "Attenuation in [9] Atkinson, C.M. and H.K. Kytomaa. 1991. "Acoustic Properties Suspensions of Irregularly Shaped Sediment Particles: A Two- of Solid-Liquid Mixtures and the Limits of Ultrasound Diagn: Parameter Equivalent Spherical Scatterer Model." Journal of the Experiments." Liquid-Solid Flows, FED. Vol. 1: 145. Acoustical Society of America, 102(3): 1485. [10] Atkinson, C.M. and H.K. Kytomaa. 1992. "Acoustic Wave [29] Guillon, L. and X. Lurton. 2001. "Backscattering from Buried Speed and Attenuation in Suspensions." International Journal of Sediment Layers: The Equivalent Input Backscattering Strength Multiphase Flow, 18(4): 577-592. Model." Journal of the Acoustical Soc of America, 109(1): 122. [11] H. K. Kytomaa, "Theory of Sound Propagation in Suspensions: [30] Goebbels, K. 1980. "Structure Analysis by Scattered Acoustic A Guide to Particle Size and Concentration Characterization." Radiation." Research Techniques in Nondestructive Testing, Powder Technology, 82: 115-121. Vol. IV, (edited by R.S. Sharpe), Academic Press, New York. [12] Holmes, A.K. and R.E. Challis. 1999a. "Acoustic Wave [31] Egle, D.M. 1981. "Diffuse Wave Fields in Solid Media." Propagation in Silica Sols and Gels." Langmuir, 15: 3045-3049. Journal of the Acoustical Society of America, 70(2): 476. [13] Holmes, A.K. and R.E. Challis. 1999b. "The Applicability of [32] Weaver, R. and W. Sachse. 1995. "Diffusion of Ultrasound in a Acoustic Wave Propagation Models to Silica Sols and Gels." Glass Bead Slurry." Journal of the Optical Society of America, Journal of Colloid and Interface Science, 216: 50-58. [14] Dukhin, A.S. and P.H. Goetz. 1999. "Characterization of [33] Page, J.H., I.P. Jones, H.P. Schriemer, M.L. Cowan, P. Sheng, Chemical Polishing Materials (monomodal and bimodal) by and D.A. Weitz. 1999. "Diffusive Transport of Acoustic Waves Means of Acoustic Spectroscopy." Colloids and Surfaces A: in Strongly Scatering Media." Physica B, 263-264:37-39. Physicochemical and Engineering Aspects, 158: 343-354. [34] Page, J.H., M.L. Cowan, P. Sheng, and D.A. Weitz. 2000. [15] Scott, David M., Baxman, Aurthor, Jochen, C. Edwin, "Acoustic "Diffusing Acoustic Wave Spectroscopy of Fluidized Measurements of Sub-Micron Particles", Part. Part Syst. Suspensions." Physica B, 279:130-133. Charact. 12 (1995) 269-273. [35] P. D. Panetta, B. J. Tucker, R. A. Pappas, and S. Ahmed, [16] Scott, David M., Baxman, Aurthor, Jochen, C. Edwin. 1995. "Characterization of Solid Liquid Suspensions Utilizing "In-Line Particle Characterization", Part. Part Syst. Charact. Ultrasonic Measurements," IEEE Measurement Science and Technology, 2003. [17] Scott, David M. 2003. "Ten years of industrial application of In- [36] Rosny, Julien De and Roux, Philippe, "Multiple scattering in a line Acoustic spectroscopy" Particulate Systems Analysis 2003. reflecting cavity: Application to fish counting in a tank", Journal [18] Spelt, P.D.M., M.A. Norato, A.S. Sangani, and L.L. Tavlarides. of the Acoustical Soc of America, 115 (1) January 2004: 31-34. 1999. "Determination of Particle Size Distribution from [37] Rosny, Julien De and Roux, Philippe, "Reply to Comment on Acoustic Wave Propagation Measurements." Physics of Fluids, Multiple scattering in a reflecting cavity: Application to fish counting in a tank", Journal of the Acoustical Society of [19] Davis, M.C. 1979. "Attenuation of Sound in Highly America, 109 (6) June 2001: 2587-2597. Concentrated Suspensions and Emulsions." Journal of the [38] Rosny, Julien De, Roux, Philippe, and Fink, Mathias, « Field Acoustical Society of America, 65(2): 387. fluctuations spectroscopy in a reverberant cavity with moving [20] Waterman, P.C. and R. Truell. 1961. Journal of Mathematical scatterers", Phys Rev Letters, Volume 90, number 9, March 7, Physics, 2: 512. [21] Varadan, V.K., V.V. Varadon, and Y. Ma. 1985. "A Propagator [39] Cowan, M. L. Jones, I. P. Page, J. H. and Weitz, D. A., Model for Scattering of Acoustic Waves by Bubbles in Water." "Diffusing acoustic wave spectroscopy", Physical Review E, Journal of the Acoustical Society of America, 78(5): 1879. Volume 65, 66605-1-11, 2002. [22] He, D. and A.E. Hay. 1993. "Broadband Measurements of the [40] Turner, J.A. and R.L. Weaver. 1994a. "Radiative Transfer of Acoustic Backscatter Cross Section of Sand Particles in Ultrasound." Journal of the Acoustical Society of America, Suspension." Journal of the Acoustical Society of America, [41] Turner, J.A. and R.L. Weaver. 1994b. "Radiative Transfer and [23] Hay, A.E. 1991. "Sound Scattering from a Particle-Laden, Multiple Scattering of Diffuse Ultrasound in Polycrystalline Turbulent Jet." Journal of the Acoustical Society of America, Media." Journal of the Acoustical Soc of America, 96(6): 3675. [42] Turner, J.A. and R.L. Weaver. 1995. "Time Dependence [24] Crawford, A.M. and A.E. Hay. 1993. "Determining Suspended Multiply Scattered Diffuse Ultrasound in Polycrystalline Sand Size and Concentration from Multifrequency Acoustic Media." Journal of the Acoustical Soc of America, 97(5): 2939. Backscatter." J. of the Acoustical Soc of America, 94(6): 3312. [43] Turner, J.A. and R.L. Weaver. 1996. "Diffuse Energy [44] Robert J. Urick, "Principles of underwater sound", 3e, Mc Graw Propagation on Heterogeneous Plates: Structural Acoustics Radiative Transfer Theory." Journal of the Acoustical Society of America, 100(6): 3686.

Source: http://www.vims.edu/~cfried/cv/2012/Panetta_etal_2012_Oceans.pdf